Rall_Power

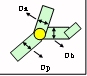
Rall value is computed as the best value that fits the equation (Bif_Dia)^Rall=(Daughter1_dia^Rall+Daughter2_dia^Rall). According to Rall’s rule we compute rall’s power by linking the diameter of two daughter branches to the diameter of the bifurcating parent. We compute the best fit rall’s power within the boundary values of [0, 5] at incremental steps of 1000 compartments. The final rall value is the idealistic n value that can propagate the signal transmission without loss from the starting point to the terminal point in a cable model assumption.

Function Output Type : Real

Calculated : At each bifurcation point

Returns a value : For each branch

Command Line Usage Function : "-f28, 0, 0, 10.0"

Output:

Metric	Total_Sum	#Compartments (considered)	#Compartments (discarded)	Minimum	Average	Maximum	S.D.
Rall_Power	14	12	(1542)	0.195	1.17667	2.41	0.532676

*All units are number

Values to consider : All

Output Interpretation :

The Total_Sum doesn't make any sense.

Total_Sum = 14 gives Total_Sum, Minimum = 0.195 gives minimum, Maximum = 2.41 gives maximum for given input neuron.

References :

Minimum, average and maximum values are meaningful for Rall's power.