Fractal_Dim

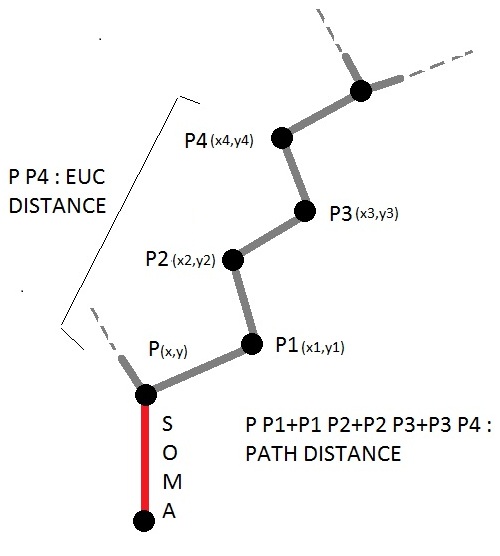
Fractal_Dim
Fractal dimension (D) of neuronal branches is computed as the slope of linear fit of regression line obtained from the log-log plot of Path distance vs Euclidean distance.

This method of measuring the fractal follows the reference given below by Marks & Burke, J Comp Neurol. 2007.
-When D = 1, the particle moves in a straight line.
-When D = 2, the motion is a space-filling random walk
-When D is only slightly larger than 1, the particle trajectory resembles a country road or a dendrite branch.




The slope of line of regression is computed using.
Slope(b): Σlog( 1+e  i )log(1+p  i )
Σlog( 1+e  i ) 2

   ( e  i is EucDistance and p  i is PathDistance)

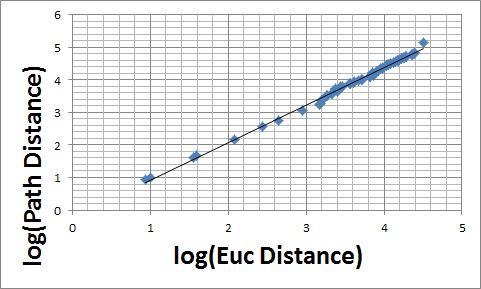Soma_Surface Example of log-log plot with log(path distance) Y-axis and log(euc distance) on the X-axis.
























Function Output Type : Real

Calculated : At each bifurcation point

Returns a value : For each branch

Command Line Usage Function : "-f44, 0, 0, 10.0"

Output:
Metric Total_Sum #Compartments
(considered)		 #Compartments
(discarded)		 Minimum Average Maximum S.D.
Fractal_Dim 63.0196 60 (892) 1.00167 1.05033 1.16165 0.03943

Values to consider : All

Output Interpretation :

Total_Sum = 63.0196 gives Total_Sum, Minimum = 1.00167 gives minimum, Maximum = 1.16165 gives maximum for given input neuron.


References :
-The Branch needs at least 3 compartments or 4 endpoints to compute the Fractal_Dim.
-Most of the meandering branches have an average value of fractal dimension (D) = 1.05